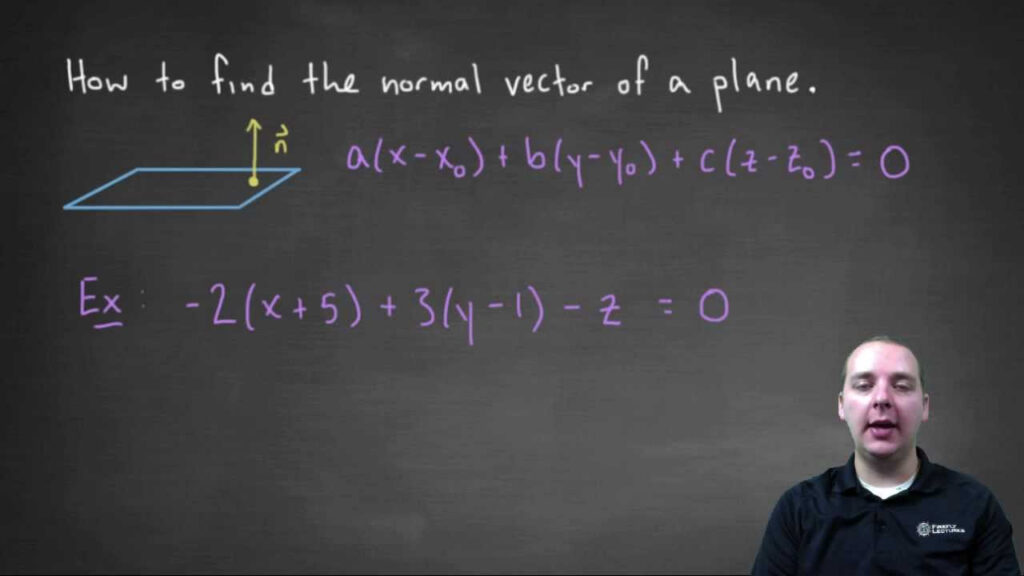In calculus, a plane is a flat, two-dimensional surface that extends infinitely in all directions. The general form of a plane equation in three-dimensional space is represented as Ax + By + Cz + D = 0, where A, B, and C are the coefficients of x, y, and z, respectively, and D is the constant term.
This equation is known as the general form of a plane because it represents all possible planes in three-dimensional space. By manipulating the coefficients and constant term, we can determine the orientation, position, and distance of a plane from the origin.
General Form Of Plane Cal
How to Identify the General Form of a Plane
To identify the general form of a plane, you need three non-collinear points or a point and a normal vector. Using these points or vectors, you can determine the coefficients A, B, and C by solving a system of equations. Once you have the coefficients, you can write the equation in the general form Ax + By + Cz + D = 0.
For example, if you have the points (1,2,3), (4,5,6), and (7,8,9), you can find the normal vector by taking the cross product of the vectors formed by the points. Then, you can use the normal vector and one of the points to find the coefficients A, B, and C. Finally, you can plug these values into the general form equation to represent the plane.