The Point Normal Form Of Plane

What is Point Normal Form?

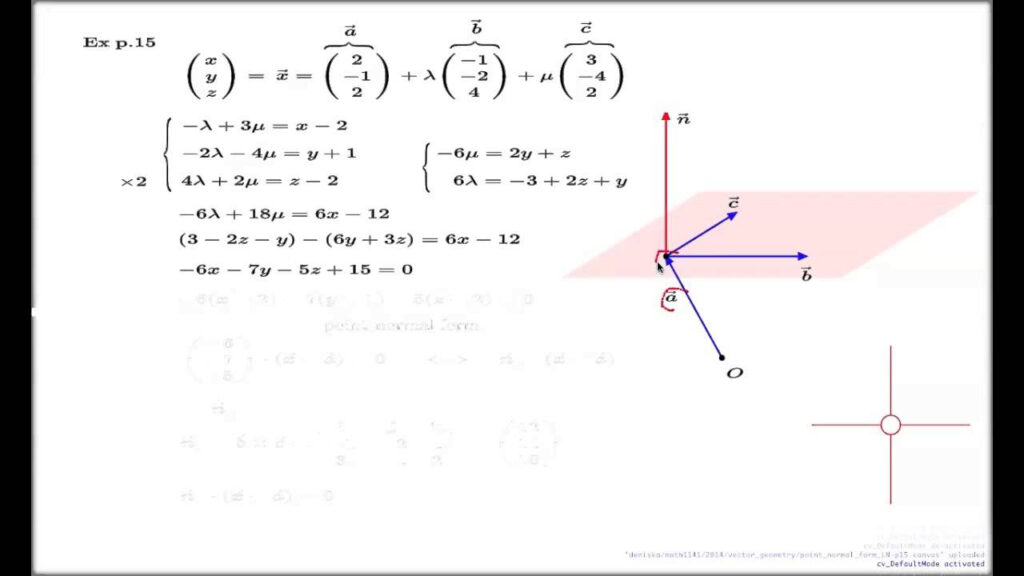
Point Normal Form is a way to represent a plane in three-dimensional space using a point on the plane and a normal vector to the plane. The equation of a plane in Point Normal Form is given by:
a(x – x0) + b(y – y0) + c(z – z0) = 0, where (x0, y0, z0) is a point on the plane and (a, b, c) is a normal vector to the plane.
This form is particularly useful in geometry and physics for defining planes and calculating distances between points and planes.

How to Convert to Point Normal Form?

To convert the equation of a plane from standard form (Ax + By + Cz + D = 0) to Point Normal Form, you need to find a point on the plane and a normal vector to the plane.
1. Choose a point (x0, y0, z0) on the plane.
2. Find the normal vector by taking the coefficients of x, y, and z in the standard form equation (a, b, c in Point Normal Form).
3. Substitute the point and normal vector into the Point Normal Form equation to get the final equation of the plane.

Applications of Point Normal Form

Point Normal Form is widely used in computer graphics for rendering 3D objects, in robotics for path planning and collision detection, and in engineering for defining planes in 3D space.
Understanding Point Normal Form can help in solving problems related to geometry, physics, and spatial relationships between objects in three-dimensional space.