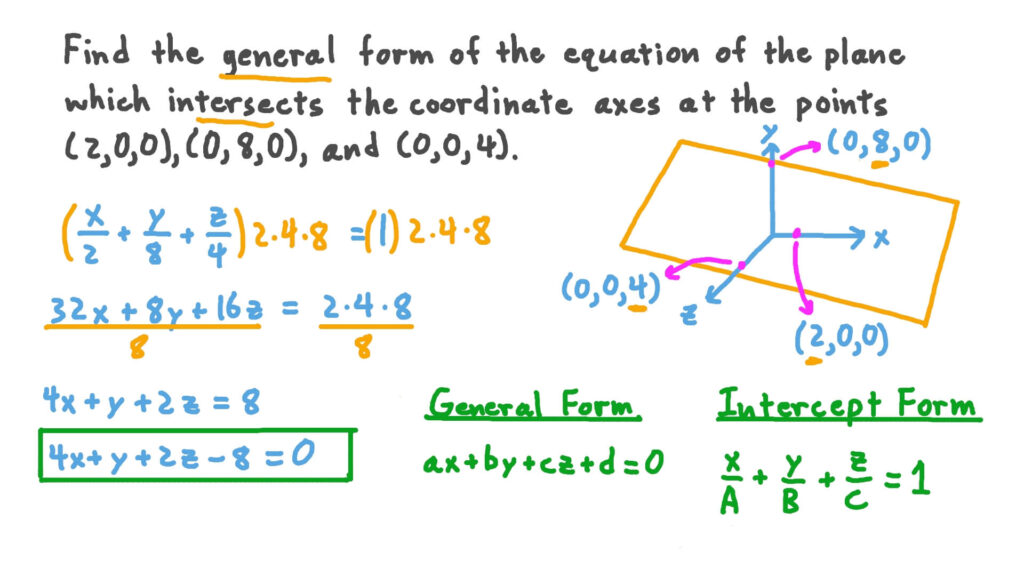
The general form of a plane is a mathematical equation that represents a plane in three-dimensional space. It is written as Ax + By + Cz + D = 0, where A, B, and C are the coefficients of the x, y, and z variables, and D is a constant term. This equation describes all the points that lie on the plane.
Each coefficient in the equation has a specific meaning. A, B, and C represent the direction vector of the plane, while D is the distance of the plane from the origin. By manipulating the coefficients, you can shift, rotate, or scale the plane in space.
General Form Of A Plane
How to Convert Other Forms to the General Form
There are several ways to convert other forms of a plane equation to the general form. One common method is to start with the point-normal form of the equation, which is Ax + By + Cz = D, where (A, B, C) is the normal vector to the plane and (x, y, z) is a point on the plane. By rearranging terms and simplifying, you can convert this equation into the general form.
Another approach is to convert the symmetric form of the equation, which is (x – x0) / a = (y – y0) / b = (z – z0) / c, where (x0, y0, z0) is a point on the plane and (a, b, c) is the direction vector of the plane. By expanding and simplifying this equation, you can obtain the general form.
Conclusion
The general form of a plane is a fundamental concept in three-dimensional geometry. By understanding this equation and its properties, you can effectively work with planes in space and solve various geometric problems. Whether you are studying mathematics, physics, or engineering, mastering the general form of a plane is essential for your success.