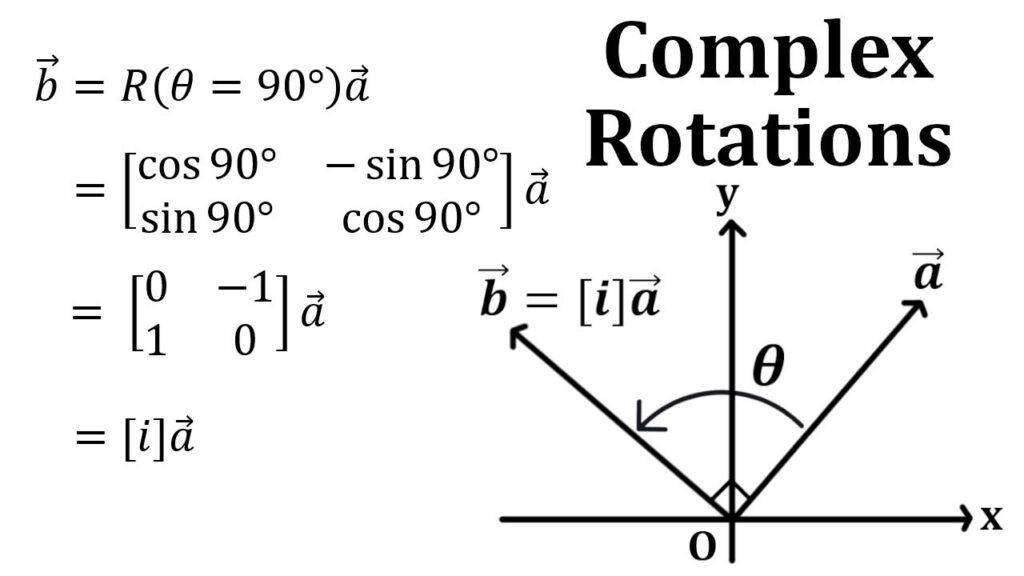
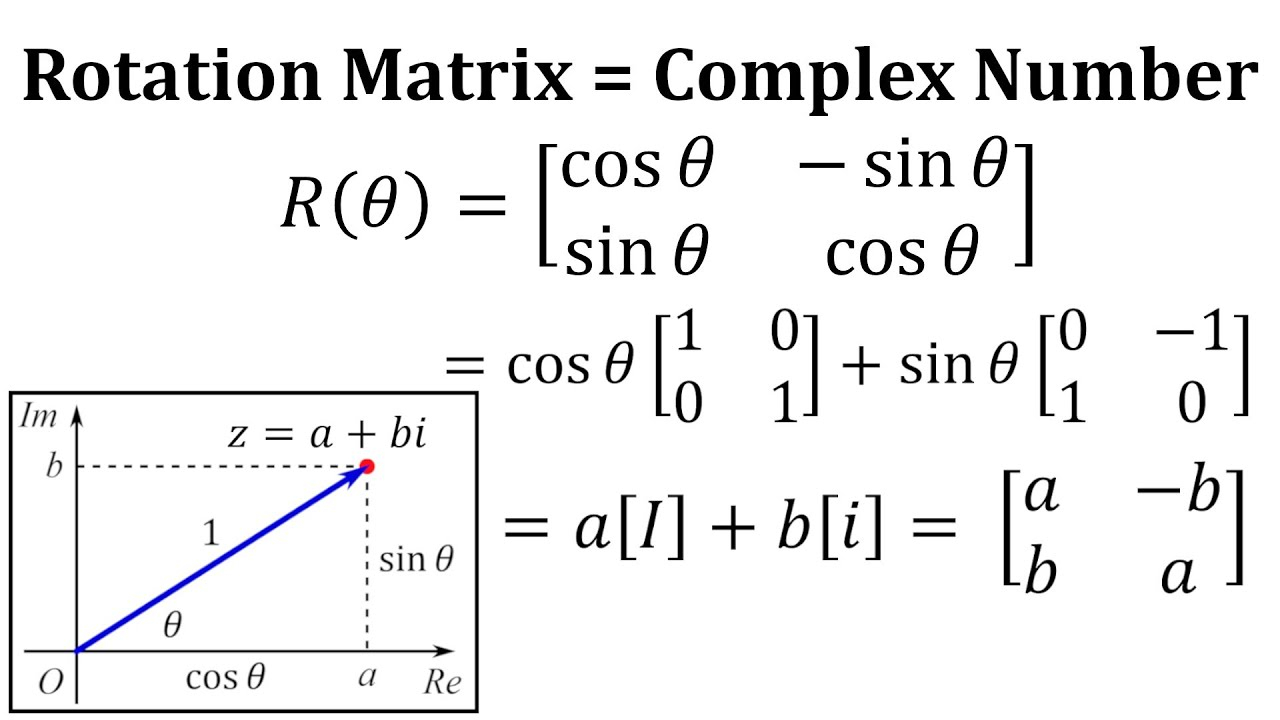A plane rotation matrix is a mathematical representation of a rotation in a two-dimensional plane. It is used to describe the orientation of an object in space relative to a fixed reference frame. The rotation matrix consists of a set of numbers arranged in a specific way that allows for the transformation of coordinates from one frame of reference to another.
The plane rotation matrix form can be represented as:
Plane Rotation Matrix Form
$$
beginbmatrix
cos(theta) & -sin(theta)
sin(theta) & cos(theta)
endbmatrix
$$
How is the Plane Rotation Matrix Form Used?
The plane rotation matrix form is commonly used in computer graphics, robotics, and other fields where rotations in a two-dimensional plane need to be represented mathematically. It allows for efficient calculation of transformations without the need for complex trigonometric functions.
By applying the rotation matrix to a set of coordinates, one can easily rotate an object around a specified angle. This is particularly useful in computer graphics for tasks such as rotating images, objects, or animations.
Conclusion
In conclusion, the plane rotation matrix form is a powerful tool for representing rotations in a two-dimensional plane. Its simple yet effective structure makes it ideal for various applications in mathematics, computer science, and engineering. By understanding how to use and apply the rotation matrix, one can easily manipulate objects in space with precision and accuracy.